Even when the theory was copacetic the data often weren't, experimental science being what it is. Telescopes are famously ill-tempered instruments even in modern times, as Hubble demonstrated when it was switched on in 1990. The idea of sharing data is also a relatively new invention. Kepler's brilliant insights were made possible by Tycho Brahe's observations, but only after he pried them from Tycho's cold dead fingers. And for much of history, astronomy data came with other occupational hazards. Merely suggesting the Earth wasn't the center of the universe would get you a stern lecturing from the village vicar if not a visit from the Inquisition. Back in the day, it didn't take the United States Congress to impede scientific progress.
The net result is anyone (read: LabKitty) trying to decipher this mess faces a mountain of hinky information. What would be helpful would be a helpful guide. A Sherpa familiar with the path to the summit. Alas, most astronomy resources are written by people who love astronomy, and that love blinds them to how impenetrable their lingo and systems of measurement appear to an outsider. Any reasonable person would just leave them be and move on to more welcoming intellectual climes. By now you know LabKitty is not one of those.
As such, I assembled a great pile of notes as I combed through various astronomy articles, on-line and otherwise, translating their arcane arcanology and mystifying calculations into my own understanding, however imperfect that may be. It occurred to me rather than committing these notes to the incinerator now that my orrery is complete, others might benefit from them. Ergo, I have condensed them into a more readable form (albeit removing most of the swear words) which I present below in the hopes someone might care to read and learn from them.
The result is rather lengthy. I encourage you to view this as a Good Thing. I can make my orbital mechanics summary short and then each sentence is dense and potentially hard to follow. Or, I can make my summary long and add lots of words that hopefully keep the train of thought from derailing. I've taken the latter approach. I creep up on the finished product a piece at a time, starting with the simplest possible description of orbital motion that is gradually made more complicated but more accurate. I pause to review equations when they are introduced, such as the equation of an ellipse. On the other hand, I'm happy to punt when showing details would grind things to a halt without adding much in the way of understanding. For example, I just write down the result for rotation transformations because the derivation is a thicket of trigonometry. I show you how to use Kepler's equation but I don't derive it. And instead of trying to explain the various calendars used in astronomy, I just pick one and give you some Javascript that does the necessary time conversion, mostly because I gave up trying to understand the various calendars used in astronomy.
Lastly, I attempt to tame the bizarre terminology that has attached itself to the astronomy literature. I write an important term in italics when it first appears, and important but strange astrowonk lingo in bold italics. I suspect you have encountered many of the italics terms before, but you may have not encountered any of the bold italics terms. You want to be wary of bold italics terms because it's easy to get lost in the arcane lexicon they form.
To reiterate: Good Thing. There's nothing that says you must read this in one sitting. In fact, if you repeatedly return over the course of several days I get more page hits. I don't know how that benefits me but Google assures me it is so.
Well, then. Enough introduction. Grab yourself a beverage and let's get this party started.
The Big Picture
Here's what we're after: Pick a date of interest (henceforth: DoI). For that DoI, draw a picture of the solar system -- that is, how the solar system appears when viewed from afar. This is the concept of an orrery, as opposed to the concept of ephemeris, the latter describing locations in the night sky and the former describing locations using some ginormous (x,y,z) solar system coordinates centered at the sun.
Obviously, to do this we need to find out the locations of everything. I'll focus on the planets here, but an orrery can contain anything you like -- planets, moons, comets, spaceships, whatever. Given infinite money, here's how we might obtain the necessary data:
1) fly out to some distant location on a spaceship
2) take a picture of the solar system and make a note of the date
3) write down the governing equations of motion of all the planets
4) using 2 as the initial condition, solve 3 at your DoI
There's a problem with this approach. We can write down the equations of motion for the planets but a) they're only approximate and b) we can't solve them anyway. As a result, we are forced into a compromise. A few thousand years of observational data exists describing the positions of the planets and whatnot. Spacewonks have converted these observations into a collection of orbital data and fit curves to it. Descriptions of these curves are published in various astronomy sources. So we can, in principle, get the position of a planet at any time by interpolation, at least to some reasonable degree of accuracy.
2) take a picture of the solar system and make a note of the date
3) write down the governing equations of motion of all the planets
4) using 2 as the initial condition, solve 3 at your DoI
We need to understand these astronomy curve fitting equations. However, curve fitting is just the beginning of the story. The equations don't give you global (x,y,z) coordinates in one fell swoop, they spit out local orbit coordinates which must be converted into global (x,y,z) or whatever you require. A given application may involve multiple orbits -- an orrery of the planets contains at least eight -- some or all of which may be oriented in different directions. We need to define a "master" coordinate system and figure out how to convert coordinates expressed in local orbital coordinates into our master system so multiple planets can be drawn in the same figure or otherwise compared.
In short, we need to understand how the astronomy community describes an orbit. As I hinted at above, this involves some rather odd terminology. It also involves some rather odd calculations, Nature stepping in to make the math more complicated than we might like. Let's see if we can't sort this out anyway. We'll begin with the simplest possible description of one thing orbiting another, after which we will incrementally add complications that are needed to make our description jive with what really goes on up in the sky.
We begin with a circle.
This Thingy Goes Around that Thingy
The simplest description of one thing orbiting another is a circle, with the thing doing the orbiting (i.e., the satellite) moving at constant speed around a central body and completing one orbit every so many whatevers (usually days). Here's a picture:
We would like to describe the position quantitatively, so we include a coordinate system. The natural place for the origin is at the center of the orbit. We then pick some distant bright star and draw a line between the center and that star. That defines an x-axis. The y-axis is chosen as a direction orthogonal to the x-axis. Easy peasy.
For example, if we were describing the Earth orbiting the sun, the sun would be at the center and Earth would be tracing out a circle with a radius of 149.6 million kilometers. It's a pain to write "149.6 million kilometers" all the time so astronomers defined the astronomical unit (AU, also abbreviated au, a.u., and ua) where 1 AU = 149.6 million kilometers and we say the orbit of Earth has a radius of 1 AU (actually the radius is only approximately 1 AU, for reasons we'll get into later). The Earth makes one orbit in one year, or, to be a little more precise, 365.25 days (the 0.25 is why there's leap years). We say Earth has an orbital period of 365.25 days.
If we knew one date when the Earth crossed the x-axis, we could compute the position of Earth for any other date simply by computing the elapsed time from last x-axis crossing modulo 365.25 days divided by the orbital period and multiplied by 360 degrees. That gives us a reference angle (call it θ) measured counterclockwise from the x-axis. We then compute (x,y) coordinates using x = r ⋅ cos(θ) and y = r ⋅ sin(θ) where r = 1 AU.
It would be nice if things were that simple. It turns out that description doesn't quite jive with the way planets actually move. We need to tweak our description to make it agree with what you see in the sky and read in the astronomy textbooks. This tweaking comes in the form of a half dozen or so complications. Some of these are forced upon us by Nature. Some of these we did to ourself.
Complication #1 -- Orbits are Not Circular
As Johannes Kepler discovered, orbits are not circular -- they're elliptical. So instead of the picture above, we really have something more like this:
Two points of interest: 1) the orbit is no longer a circle, and 2) the sun (or whatever) is at a focus of the ellipse not at the center. We will have much to say about elliptical orbits and using them to compute planet positions before we are done. However, let us pause here and review the humble ellipse before continuing.
As you probably recall, the equation of an ellipse is given as:
x2/a2 + y2/b2 = 1
The ellipse crosses the positive x-axis at (a,0) and crosses the positive y-axis at (0,b), defining the semi-major axis and semi-minor axis, respectively (2a and 2b are thus the major axis and minor axis, respectively). If b = a, the ellipse equation reduces to x2 + y2 = a2, which is the equation of a circle having radius a. Ergo, an ellipse can be thought of as a generalization of a circle. Whereas a circle is the set of all points equidistant from the center, an ellipse is the set of all points whose sum of the distance to the two focal points is constant. The focal points (plural: foci) are located at (+f,0) and (-f,0). When the ellipse describes an orbit, something (e.g., the sun) occupies one focus and the other focus is empty.
The "circleness" (or lack thereof) of an ellipse is quantified using a single number called the eccentricity (e). We have 0 ≤ e < 1 (note the strict inequality on the right -- if e = 1 we have a parabola instead of an ellipse). A circle is an ellipse with eccentricity zero. The closer e is to 1, the more squashed the ellipse As you might expect, e is related to a and b:
e = ( √ 1 − (b/a)2 )
This relation appears in astronomy calculations in various equivalent forms. The focal distance (i.e., the distance from the center to either focus) is given by f = a ⋅ e, or, equivalently, f = √ (a2 − b2).
Footnote: There's an old timey way of defining an ellipse as the intersection of a cone and a plane, which then defines eccentricity in terms of something called a directrix. I will steer clear of this crazy talk, as should you.
For many astronomy applications, the ellipse is much ado about nothing. Although eccentricity can be large for comets and other small bodies, it's tiny for the planets. Tiny, tiny, tiny. We could assume planet orbits are circular (e = 0) and the error introduced would probably be negligible. For example, I mentioned Earth's radius is only approximately 1 AU. The published value is 1.000003 AU, which is an average over one year and is greater than 1 due to the eccentricity of the orbit. Clearly the eccentricity is tiny. However, astronomy sites all include a nonzero e in their data, I guess because the other astronomers would make fun of them if they didn't. We need their data, so we have to play their game.
Complication #2 -- Planet Motion is not Uniform
Kepler's second great discovery was that a satellite does not move at a constant speed as it traces out its orbit ellipse. The satellite moves faster when it is closer to the central body and moves more slowly when it is farther away. In particular, it is moving fastest when it crosses the positive x-axis and slowest when it crosses the negative x-axis; these special points are called the perihelion and aphelion, respectively (the usual convention is to put the central body at the positive focal point).
Footnote: It's called the perihelion and aphelion when the central body is the sun; for something orbiting the Earth, the terms perigee and apogee are used instead.
Non-uniform speed is a pain. When I introduced the circular orbit, I noted it's relatively easy to compute the position of the satellite if you know one time when it crossed the x-axis (more properly, the time of perihelion). You just compute elapsed time modulo the orbital period, then divide by the orbital period and multiply by 360 degrees. That doesn't work if the speed isn't uniform.
Fortunately, Kepler provided an equation to help us out. The general idea is we begin by assuming the motion is uniform to get an approximate position. We then apply a correction to get the true position. To explain this I need a figure:
I will describe this figure using slightly incorrect terminology which I will then correct in the next paragraph. What we would like to calculate is the "true" position of the satellite (e.g., planet), here labeled T. The true position lies somewhere on the orbit ellipse. We can't calculate that knowing only the time to last perihelion, but we can use that information to calculate an approximate or "mean" position of the planet by assuming the orbit is a circle of radius a. I've labeled this M. By applying Kepler's equation, we obtain an "eccentric" position from the mean position, here labeled E. Note a vertical line dropped down from E intersects T, so once we obtain the eccentric position, we can obtain the true position with a bit of trigonometry. I should note the above figure greatly exaggerates these effects -- as I noted earlier the orbits of the planets are all nearly circular, in which case T, M, and E coincide.
Now to correct the terminology. Kepler's equation doesn't work with positions, it works with angles. And astronomers don't use the term "angle," they use the term anomaly. I don't know why. So instead of the true position, we have the true anomaly, which is the true position of the planet measured as the angle afT. We also speak of the eccentric anomaly which is the angle aOE and the mean anomaly which is the angle aOM. Note the true anomaly is measured from the focus of the orbit (probably the sun) and the other two angles are measured from the center. I will continue to refer to these as T, E, and M, although I really mean the angles afT, aOE, and aOM.
An example might help clarify these concepts. Suppose the orbital period of a planet is 80 days and it is now 10 days since last perihelion. You might think it has completed 10/80 or 1/8 of its orbit (i.e., 360/8 = 45 degrees). The mean anomaly is indeed 45 degrees. However, planets move faster when closer to perihelion, so it has actually moved farther than 45 degrees in these 10 days, so the eccentric anomaly is greater than 45 degrees. I'll compute the eccentric anomaly for this example below, after describing Kepler's equation.
Once we have the eccentric anomaly, we can get the true anomaly (an angle) using some arctangents and whatnot. However, if we're just interested in what I have called the true position (a location), that's straightforward to calculate from the eccentric anomaly. We have:
x = a ⋅ cos(E)
y = b ⋅ sin(E)
There's a clever way of remembering these equations. Superimpose a circle with radius a and another with radius b on the ellipse:
That should help you see where x = a ⋅ cos(E) and y = b ⋅ sin(E) come from.
What remains is to show how to obtain the eccentric anomaly from the mean anomaly. This is done using Kepler's equation:
M = E − e ⋅ sin(E)
Here, M and E are in radians. Immediately we run into weirdness. It is easy to use Kepler's equation to find M given E. But we need to go in the other direction. We need to find E given M. It turns out you can't solve Kepler's equation for E algebraically, although mathozoids have derived solutions based on some horrific Taylor series expansion. A simpler approach is to solve the equation numerically using iteration. That is, you set E = M, then repeatedly update E = M + e ⋅ sin(E) until E stops changing to however many decimal places you need. You can easily do this on a calculator.
Let's apply this to the example I started above. If we assume e = 0.1 and a mean anomaly of 0.785 radians (i.e., 45 degrees), then after three iterations of Kepler's equation I obtain an eccentric anomaly of 0.861 radians or 49.3 degrees. The planet has moved farther than the mean anomaly because it moves faster when closer to perihelion.
Footnote: As I understand it, iterative solutions of Kepler's equation usually behave themselves if e is small, but if e is close to 1 numerical problems sometimes appear (i.e., the solution will converge slowly, or won't converge at all). Consider yourself warned.
Footnote: Sometimes you see a different form of Kepler's equation that uses M and E in degrees: M = E − (180/π) e ⋅ sin(E). This looks like we're converting eccentricity to radians, which should be making you confused because eccentricity is dimensionless. Here's the story: Multiply both sides of M = E − e ⋅ sin(E) by (180/π) to get: (180/π) M = (180/π) E − (180/π) e ⋅ sin(E). However, (180/π) M is just M expressed in degrees and (180/π) E is just E expressed in degrees. So when we write E and M in degrees, the leading constant vanishes in these terms and we are left with M = E − (180/π) e ⋅ sin(E). The new equation isn't wrong, it's just bad notation. Astronomers should really use different symbols here.
Footnote: Kepler's observations are summarized as Kepler's Three Laws of Planetary Motion. In simplified form: 1) orbits are elliptical, 2) motion is not uniform, and 3) orbital period increases with orbit size. Kepler's equation is not one of Kepler's Laws, but it can be derived from them.
The various anomalies allow us to calculate the position of a planet in its orbit. However, we are often interested in describing the orbits of many things simultaneously. For example, the solar system has eight planets and much else besides and we might want to compare their relative positions or plot them all in one figure. Eventually we will pick a special "master" coordinate system and express all the data in that. First, however, we need to understand how the orientation of an orbit is defined, and how to take a position expressed in one coordinate system and transform it into another.
Complication #3 -- Orbit Orientation
We require two parameters to define the orientation of an orbit: 1) the direction of its major axis and 2) the inclination of the plane of the orbit. First, consider the direction of the major axis. We have the following:
As shown here, the major axis of an orbit is not necessarily oriented in the x-direction. We must specify the mean longitude of the orbit, as measured from some chosen reference direction. (We say "mean" longitude and not just "longitude" because it drifts around over time, as will be described in a later complication.) I've used the Greek letter ϖ to denote this angle. However, orbit orientation is commonly listed in astronomy tables as the sum of two other angles. I can't explain those until I describe inclination. We have the following:
Not only can the major axis of an orbit point in an arbitrary direction, the plane of the orbit can be inclined with respect to the plane of another. We quantify this using the angle of inclination usually denoted using the Greek letter α. We define a reference plane having zero inclination and so the angle of inclination of an orbit of interest is defined with respect to that reference. In our solar system, the reference plane is called the ecliptic (or ecliptic plane) and passes through the center of the sun. The coordinates system defined by the ecliptic are called ecliptic coordinates. Earth's local orbit coordinates are almost but not quite the same as ecliptic coordinates, due to some historical weirdness we'll get into in just a moment.
Footnote: Inclination can be large for comets and other small satellites, but, like eccentricity, it's generally tiny for the planets. When the solar system formed, the planets all condensed from the same bunch of space junk going around the sun and as a result their orbits ended up more or less coplanar. However "more or less" coplanar is not "exactly" coplanar, and orbital data listed in various astronomical tables typically includes a small but finite inclination. We need their data, so we have to play their game.
Footnote: Pronounced "e-kliptik."
Knowing the inclination of an orbit and the longitude of the major axis allows us to completely define its orientation. However, there's one final twist. Even though I've drawn the axis of inclination coincident with the y-axis in the figure above, the axis of inclination can generally be located anywhere in the orbit. We need a way to nail it down.
Clearly, if an orbit has an inclination, a satellite in that orbit spends part of the time above the ecliptic plane and part of the time below it. The location in the orbit at which the satellite crosses the ecliptic moving from below to above is called the ascending node, and the angle of inclination is measured at that location. This is not merely a convention; if you chase around the trigonometry, you'll find that the location of the ascending node affects the various coordinate transformations we need later.
Finally, I can now describe the orientation of the major axis as it's usually specified in astronomy tables. Here's a picture:
Astronomy tables typically don't list the longitude of perihelion (i.e., the direction of the semi-major axis), they list the longitude of the ascending node, measured counterclockwise from a reference direction. The longitude of perihelion is defined relative to the longitude of the ascending node using an angle called the argument of perihelion (or argument of periapsis when describing an Earth-centered orbit). The longitude of the ascending node is denoted in many sources using the Greek letter Ω. The argument of perihelion is denoted using the Greek letter ω. The longitude of perihelion is denoted using the Greek letter ϖ. A few astronomy resources list ϖ, but more commonly you simply compute it: ϖ = Ω + ω. Yes, this is a mess. No, it's not my fault.
Footnote: The ascending node is usually labeled on astronomy diagrams with a tiny pair of headphones. I don't know why.
We now know how to describe the orientation of an orbit. All that's left to do is pick a master coordinate system we will use when dealing with data from two or more orbits. A simple idea would be to use Earth's orbit. As we have seen, Earth's orbit is already used to define the AU, so why not use it to define the reference longitude and inclination? You might think astronomers are sensible folks and so this is what they did.
Think again.
Complication #4 -- The First Point of Aries
Earth's orbital plane is used to define the ecliptic. That is, the inclination of Earth's orbit is zero by definition. This is not true for the other planets, and a transformation is applied to express everybody's position in ecliptic coordinates when considering a collection of orbiting things. More on transformations in a bit.
The direction of zero longitude is another story. A sensible selection would have been the positive semi-major axis of Earth's orbit. Instead, zero longitude is defined by the position of Earth at the vernal equinox.
That may sound redonkulous, but there's an explanation. Astronomy data has a long history and ancient astronomers had no idea about elliptical orbits and perihelions and the Internet. All they could do was observe stuff on Earth. And as the Earth goes around the sun, stuff on Earth changes. Notably, the length of the day changes. The ancients may not have known why this happens, but they recorded it obsessively. Eventually somebody noticed there were two days each year when the length of the day and the length of the accompanying night were equal (both exactly 12 hours, give or take). The one in the spring (in the northern hemisphere) they called the vernal equinox. They noted of the path of the sun in the sky on the equinox, then 12 hours later (when it was dark) they noted the constellation Aries moved along the same path. Expressing observational data relative to this became the norm. Thus was the direction of zero celestial longitude defined.
Here's a picture:
What I'm trying to illustrate is the position of Earth at the vernal equinox relative to a few constellations (some of my constellations might not be accurate). The Earth moves around, but the positions of the constellations are fixed. What's important is that on the date of the vernal equinox, a line drawn between the sun and the Earth would point out toward the constellation Aries, or at least it did when Ptolomy established the rule back in the 2nd century. Aries covers a pretty big patch of sky, so to be a little more precise Ptolomy picked a particular location in it to define the equinox, which he called the First Point of Aries.
Footnote: Because of orbit wobble (see next complication), the direction of zero longitude axis changes over time; these days it's in Pisces and will soon be in Aquarius. That doesn't matter -- the reference direction is still called the First Point of Aries.
Footnote: Neither Aries (nor Pisces) are what you would call spectacularly well-defined constellations, so I don't personally find any of this to be helpful (admittedly, the only constellation I can identify is Orion).
Footnote: All of this Aries business is why the reference axis is often labeled with a little ram's head (the astrological symbol for Aries) on astronomy diagrams.
At the end of the day, it doesn't matter what direction we pick for a reference as long as we pick one. Just like longitude on Earth, which the British arbitrarily decided should be referenced to Greenwich England. The First Point of Aries defines a system of longitude around the sun, with the vernal equinox equivalent to zero longitude. The values of orbit parameters are expressed relative to this.
Interlude -- Coordinate Transformation
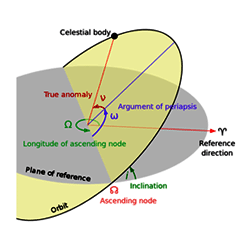
We finally have everything we need to describe the position of a planet (or any other kind of satellite) in its orbit. Here's a nice 3D summary:
 |
| Source: Wikipedia.org |
I stole this from Wikipedia* so you'll see something familiar if you start poking around over there for more information. (Actually, I stole this from Wikipedia because it saved me the trouble of making another figure. Rock on, Creative Commons!)
* Image by Lasunncty and appears here under the provisions of the Creative Commons Attribution-Share Alike 3.0 Unported license.
However, we're not just in this for the pretty pictures, we want to calculate numbers -- specifically we need to take a position expressed in local orbit coordinates (which, in general, is inclined relative to the ecliptic and oriented at some mean longitude) and express that position in ecliptic coordinates. This requires a coordinate transformation.
Here I'm going to punt.
I think you would agree the concept is not complicated (transform a point expressed in this coordinate system into the equivalent location expressed in that coordinate system) and the resulting equations are just plug-and-chug, but the derivation is a mess of trigonometry. Just trying to draw a picture gave me kittens. So, no picture and no derivation. Instead I'll just write down the equations. There are various equivalent forms of these; I'll give you the version used on the JPL website:
x = [cos(ω)cos(Ω) − sin(ω)sin(Ω)sin(α)] x'
+ [−sin(ω)sin(Ω) − cos(ω)sin(Ω)cos(α)] y'
y = [cos(ω)sin(Ω) + sin(ω)cos(Ω) cos(α)] x'
+ [−sin(ω)sin(Ω) + cos(ω)cos(Ω)cos(α)] y'
z = [sin(ω)sin(α)] x'
+ [cos(ω)sin(α)] y'
Here, α is the inclination, Ω is argument of perihelion and ω is the argument of the ascending node. The pair (x', y') is a location in the local orbit coordinates and the triplet (x,y,z) are the equivalent ecliptic coordinates.
+ [−sin(ω)sin(Ω) − cos(ω)sin(Ω)cos(α)] y'
y = [cos(ω)sin(Ω) + sin(ω)cos(Ω) cos(α)] x'
+ [−sin(ω)sin(Ω) + cos(ω)cos(Ω)cos(α)] y'
z = [sin(ω)sin(α)] x'
+ [cos(ω)sin(α)] y'
The good news is we are almost done.
The bad news is we are almost done.
Nature isn't quite finished making life difficult.
Complication #5 -- Time Dependencies
As if we don't have enough headaches already, everything about an orbit -- the reference direction, the major axis, the eccentricity, the inclination, etc. -- changes over time. Not much from day to day, but more substantially over the centuries.
The most striking change is the direction of the major axis, which is called precession (or, to be more precise, apsidal precession, to distinguish it from the precession of the rotational axis or changes in other orbital parameters). Long story short, over the eons a planet tends to trace out a spirograph looking thing. Exaggerating greatly, it looks like so:
This happens because physics. Indeed, there's actually some fairly nasty physics involved (a complete explanation requires General Relativity). The equations describing this physics are very difficult to solve. As such, the way astronomers deal with precession is more curve fitting. Not only do they interpolate the current position of a satellite in its orbit, they also interpolate the current configuration of the orbit in space. They provide fitting equations, you plug in a date of interest, and out pops interpolated values for all the orbit parameters. You then use these parameter values in your calculations.
Obviously, for this trick to work, you need to express your date of interest using the same calendar the astrowonks used to create their interpolation equations. Which raises an uncomfortable question: What year is it? You may think it's 2016, but it's 12016 according to the Holocene calendar, 1732 in the Coptic calendar, and 1437 by Islamic reckoning. The Buddhists call it 2560, the Byzantines call it 7542, and the Chinese call it either 4712, 4713, 4652, or 4653. If you think I'm being silly, remember astronomy data goes back thousands of years. Over that time, calendars have changed many times.
Which calendar should we use? You might think astronomers are sensible folks, so they created an easy-to-understand universal system of time measurement.
Think again.
A calendar is defined by picking a year zero. Astronomers call their chosen year zero an epoch, which should be offending any English speakers joining us today. In colloquial use, an "epoch" is not a time; it is a time period (e.g., the Holocene epoch, the Cretaceous epoch, the Clinton epoch). However, astronomers have bastardized the term to mean the beginning of a time period, and so here we are.
But that's not the worst of it. The worst of it is there's a dozen or so different epochs referenced in the astronomy literature, none of which are compatible and all of which are confusing. Some sources use the Julian Date, which is the number of days since Jan 1st 4713 BC (Greenwich noon, natch). Except if you're interested in a date after October 15, 1582, and then you must convert to the Gregorian calendar. Although not if you're using the Hipparcos catalog, which is based on an epoch of April 2.5625, 1991, aka J1991.25 or 8.75 Julian years before 2000 January 1.5. Unless your data is expressed in Besselian years, which are the number of years (+ fraction) since January 1st, 1950. And because this wasn't confusing enough, JPL invented their very own time (the Teph) which their astronomers have been using in publications since 1960.
Most days, I'm astonished we ever got off this rock.
The problem is nobody wants to give up their favorite epoch, and it wouldn't matter if many did because they are long dead and their data is baked into cuneiform tablets. Not exactly the most upgradable information technology. Still, the International Astronomy Police eventually stepped in and defined a standard epoch called J2000.0, which you might stupidly think is midnight January 1, 2000, but it's actually noon "terrestrial time" which apparently works out to January 1.5.
The best I can do is to translate this mess into code (specifically: Javascript). First, we create two Date objects:
var J2000 = new Date(2000,0,1);
var today = new Date();
The first call to Date( ) goes Date(y,m,d) where y is literal, m is zero-indexed, and d is a signed offset from zero (zero being the last day of the previous month). Calling Date( ) with no arguments returns the current date. You can also provide Date( ) with an hour and time zone (which default to 0 and whatever your local time zone is, respectively, if you omit them) which I suppose I really should have done but to be honest if your astronomical application needs a time resolution finer than one day, you really need to look into the details yourself.
Anyway, here's how you would compute elapsed time since J2000.0:
var elapsedTime = (today.getTime() - J2000.getTime());
Javascript's getTime( ) function traffics in milliseconds, so you divide elapsedTime accordingly to get whatever time measure your astronomy source expects. For example, dividing by (1000*60*60*24*365.25*100) gives you elapsed time in centuries, including a fractional part (this is what the tables published by JPL use). What's critical is that the elapsed time is expressed with respect to the appropriate epoch, which here (and in an increasing number of astronomy resources) is J2000.0.
Putting it all together
Finally, at last, we have all the tools we need.
If we want to compute the position of a satellite for any date -- past, present, or future -- assuming we can find the appropriate astronomy data, the steps go like this:
1) look up the epoch of the data you're using (e.g., J2000.0)
2) express your date of interest (DoI) in epoch time
3) compute orbit parameters (e, α, Ω, ω, ϖ, etc.) at the DoI
4) convert the DoI into time-since-most-recent-perihelion
5) divide #4 by (orbital period / 360) to obtain the mean anomaly (M)
6) correct M using Kepler's equation to obtain the eccentric anomaly (E)
7) use E to obtain an (x',y') position expressed in local coordinates
8) transform (x',y') into (x,y,z) expressed in ecliptic coordinates
The details vary, but these steps describe the basic idea. Step 3 will use fitting equations supplied by your source -- these can differ in accuracy or the time period covered or even in the form of the interpolation. For example, the JPL data I used to construct JOrrery is based on a two-term (i.e., linear) polynomial for the inner planets with additional corrections applied to Jupiter, Saturn, and Neptune. I have seen other sources use a fifth-order polynomial, covering a different time span and expressed in a different epoch. However, the general approach remains the same.
2) express your date of interest (DoI) in epoch time
3) compute orbit parameters (e, α, Ω, ω, ϖ, etc.) at the DoI
4) convert the DoI into time-since-most-recent-perihelion
5) divide #4 by (orbital period / 360) to obtain the mean anomaly (M)
6) correct M using Kepler's equation to obtain the eccentric anomaly (E)
7) use E to obtain an (x',y') position expressed in local coordinates
8) transform (x',y') into (x,y,z) expressed in ecliptic coordinates
Once you obtain ecliptic coordinates, you are on your own. I just plotted them in my orrery, but a popular kind of post-processing is to use the ecliptic coordinates to determine where a given satellite will appear in the night sky. This gives you ephemeris -- a description of where you can find planets and whatnot usually for the purpose of viewing them with a telescope. Computing ephemeris introduces more complications (sky location depends on your Earth location, for one) and more bizarre terminology (celestial sphere, right declination, zenith, usw.). I will leave these for others to explain, as I suspect I have taxed your patience to the breaking point just getting us this far.
To wrap things up, I will point you to some astronomy resources I have found useful.
Further Reading
While I usually find sampling a variety of authors is the best way to feel out a subject, taking such an approach to the astronomy/orbital mechanics literature is asking for trouble. This because of inconsistencies that appear, some of which I have already mentioned. The epoch, the equations, even the basic terminology used to describe orbital parameters can vary in different sources. I'll provide you a few leads into the literature, but you should be aware of the potential for confusion.
The main source I used in constructing JOrrery is the JPL site (http://space.jpl.nasa.gov/). Here's a helpful pdf on computing planet positions using JPL tables assembled by E.M. Standish of their Solar System Dynamics Group:
http://ssd.jpl.nasa.gov/txt/aprx_pos_planets.pdf
Standish covers the same material I cover here, albeit using about a billion fewer words. He also provides tables of astronomical data needed to feed the equations. There are two sets of these -- one that covers 1800 to 2050 AD at higher accuracy and a second that covers 3000 BC to 3000 AD at lower accuracy. Data are provided for all nine planets, or perhaps I should say all eight planets plus Pluto.
To give you a feel for how different authors cover the same material, here's three that more-or-less do the same thing as Standish:
http://www.math.ubc.ca/~cass/courses/m309-01a/orbits.pdf
http://www.braeunig.us/space/plntpos.htm
http://www.stargazing.net/kepler/ellipse.html
The gist is always the same: Express the date of interest in the correct calendar, do some fitting, then finish with some coordinate transformations. However, the details vary. The epoch, the fitting equations, the data table -- each author has a somewhat different approach to the problem. You may find this either illuminating or confusing.
Solving Kepler's equation is a topic unto itself. Here's a readable summary, including a brief introduction to the equation (although no derivation) and a description of several solution approaches, starting with simple iteration and moving on to more sophisticated techniques like Newton's method and power series. There's code here in QBasic (which was the style at the time) and also for Excel and the TI-80 calculator:
http://www.stargazing.net/kepler/kepler.html
If you'd like a derivation of Kepler's equation, the Wikipedia page on Kepler's law isn't too terrible:
https://en.wikipedia.org/wiki/Kepler's_laws_of_planetary_motion
Wikipedia also has an extensive collection of articles on orbital mechanics. An abridged list of pages I found useful includes angular eccentricity, apsidal precession, argument of periapsis, aries (constellation), axial precession, axial tilt, barycentric coordinate time, celestial coordinate system, eccentric anomaly, ecliptic, ecliptic coordinate system, ellipse, elliptic orbit, ephemeris time, epoch (astronomy), equatorial coordinate system, equinox, equinox (celestial coordinates), first point of aries, gregorian calendar, julian calendar, julian day, julian year (astronomy), kepler's equation, longitude of the ascending node, longitude of the periapsis, mean anomaly, orbital elements, orbital mechanics, perihelion and aphelion, solar system, terrestrial time, and true anomaly. Many of these feature some nice animated gifs that are helpful in explaining the topic.
Finally, I suppose I should recommend a textbook. The standard textbook for orbital mechanics calculations seems to be Meeus. Here's an Amazon linky:
Astronomical Algorithms, by Jean Meeus
I don't own this book (I'm a biologist, not an astronomer) and I have the feeling it's starting to get a little long in the tooth, but it's cited in many articles on orbital mechanics so I'm guessing it's something of a classic in the field. YMMV.
As per the usual disclaimer, I have no affiliation with any of the authors or institutions listed in these sources. Any errors or mistakes found here (or elsewhere) are my own.
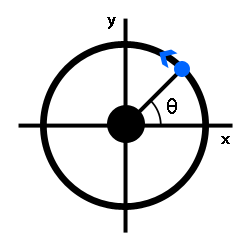
No comments:
Post a Comment