So it's Saturday night and I'm watching Brad Osgood's lectures on Fourier analysis when he writes something on the blackboard that should be familiar:
<Ax,y> = <x,ATy>
(the angle brackets indicate dot product). The point being, the matrix picks up a transpose when shifted to the other vector.
By "should be familiar," I mean should be familiar to me (maybe to you too, but I'm not judging). However, it wasn't. This ostensibly basic fact of linear algebra had suddenly arrived in my life without warning, like a stray kitten or a subpoena.
I prolly would have felt bad were it not for a gutfull of cheap vodka (what part of "Saturday night" did you not understand?). Because this looks like the kind of identity that should have been tattooed on my psyche somewhere in my undergraduate travels. Circle Pines U being what it is, I assumed here was simply yet another basic mathegonical factoid that had eluded me (or I it).
But, alas, for once my shortcomings could not be blamed on a $7/credit hour education.
Come morning, once the black mist had lifted and the voices stopped calling, I scoured my favorite resources for an explanation of the identity only to discover that, too, wasn't there. Greenberg. Mangel. Caswell. Rencher. CRC. My Schaum's library. All failed me. This apparently simple trick of the linear algebra light appeared in none.
It would seem I had to figure it out myself.
That's just rude.
You can easily derive the identity by writing out everything in component form and rearranging terms. Heck, even I got it on my first try and I have the same chance of working though a page of algebra without making a mistake as I do of winning a Sopwith Camel, which for the duration of this sentence is something I will assume people win.
Yet, algebra is not appreciation. That's not writing, that's typing, Truman Capote would chide. We seek Understanding. Enlightenment. Sobriety. We want to get inside this thing's pelt and crawl around.
Why does the matrix get transposed when shifted to y in the dot product?
A matrix-vector product can be viewed as a transformation. There the vector sits, pointing somewhere. We multiply the vector by a matrix. Now the vector points somewhere else (and maybe gets longer or shorter).
The dot product, too, has a geometric interpretation. If x and y are vectors, the dot product <x,y> gives the degree to which they are alike. Overlay. Overlap. Point in the same direction. Let us assume they both have unit length (we can always normalize them). Then "the degree to which they are alike" reduces to "the angle between them."
Hence, <Ax,y> tells us the angle between Ax and y. So does <x,ATy> as the identity demands. So why is one A transposed and the other not?
A rotation is represented by an orthogonal matrix, and one nice thing about an orthogonal matrix is the inverse is the transpose, and vice versa. Considering our quarry today is <Ax,y> = <x,ATy> you might think that clue is relevant. You would be correct.
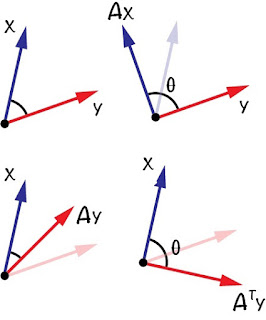
We proceed by example. An example in two dimensions, for that is the extent of my drawing skill. We have x and y in the plane like so:
Begin at upper left. The angle between x and y is given by <x,y>.
We now transform x by A. Assume the effect of A is to rotate x counterclockwise (an analogous argument holds for a clockwise rotation). As shown at upper right, the angle between x and y has increased (an analogous argument holds for a decrease). It is now given by <Ax,y>. I have assumed the transformation increases the angle between x and y to 90 degrees (denoted by θ in the figure) to make it easy to identify.
I claim we can now see why the transpose must appear if we were to instead apply A to y.
Just as Ax rotates x clockwise, so, too, does, Ay rotate y clockwise (and by the same amount). The effect of applying A to y is shown at lower left. As you can see with your eyeballs, the angle between x and y has decreased rather than increased. As such, <x,Ay> =/= <Ax,y>.
However, if we apply AT to y that rotates y clockwise because the transpose of an orthogonal matrix is the inverse and the inverse of a rotation is the rotation in the other direction. That effect is shown at lower right in the figure.
Comparing results at lower right to those at upper right, we see that the angle between the the transformed vectors (θ) is the same. That is, <Ax,y> = <x,ATy>.
So there ya go. An easy-to-remember demonstration why the transpose appears when the transformation is moved to the other vector in a dot product.
There's probably something I should write here about dual spaces and Hermitians and conjugates, but imma let you look that stuff up on your own. (Look at you, looking stuff up on your own!)
<Ax,y> = <x,ATy>
(the angle brackets indicate dot product). The point being, the matrix picks up a transpose when shifted to the other vector.
By "should be familiar," I mean should be familiar to me (maybe to you too, but I'm not judging). However, it wasn't. This ostensibly basic fact of linear algebra had suddenly arrived in my life without warning, like a stray kitten or a subpoena.
I prolly would have felt bad were it not for a gutfull of cheap vodka (what part of "Saturday night" did you not understand?). Because this looks like the kind of identity that should have been tattooed on my psyche somewhere in my undergraduate travels. Circle Pines U being what it is, I assumed here was simply yet another basic mathegonical factoid that had eluded me (or I it).
But, alas, for once my shortcomings could not be blamed on a $7/credit hour education.
Come morning, once the black mist had lifted and the voices stopped calling, I scoured my favorite resources for an explanation of the identity only to discover that, too, wasn't there. Greenberg. Mangel. Caswell. Rencher. CRC. My Schaum's library. All failed me. This apparently simple trick of the linear algebra light appeared in none.
It would seem I had to figure it out myself.
That's just rude.
You can easily derive the identity by writing out everything in component form and rearranging terms. Heck, even I got it on my first try and I have the same chance of working though a page of algebra without making a mistake as I do of winning a Sopwith Camel, which for the duration of this sentence is something I will assume people win.
Yet, algebra is not appreciation. That's not writing, that's typing, Truman Capote would chide. We seek Understanding. Enlightenment. Sobriety. We want to get inside this thing's pelt and crawl around.
Why does the matrix get transposed when shifted to y in the dot product?
A matrix-vector product can be viewed as a transformation. There the vector sits, pointing somewhere. We multiply the vector by a matrix. Now the vector points somewhere else (and maybe gets longer or shorter).
The dot product, too, has a geometric interpretation. If x and y are vectors, the dot product <x,y> gives the degree to which they are alike. Overlay. Overlap. Point in the same direction. Let us assume they both have unit length (we can always normalize them). Then "the degree to which they are alike" reduces to "the angle between them."
Hence, <Ax,y> tells us the angle between Ax and y. So does <x,ATy> as the identity demands. So why is one A transposed and the other not?
A rotation is represented by an orthogonal matrix, and one nice thing about an orthogonal matrix is the inverse is the transpose, and vice versa. Considering our quarry today is <Ax,y> = <x,ATy> you might think that clue is relevant. You would be correct.
We proceed by example. An example in two dimensions, for that is the extent of my drawing skill. We have x and y in the plane like so:
Begin at upper left. The angle between x and y is given by <x,y>.
We now transform x by A. Assume the effect of A is to rotate x counterclockwise (an analogous argument holds for a clockwise rotation). As shown at upper right, the angle between x and y has increased (an analogous argument holds for a decrease). It is now given by <Ax,y>. I have assumed the transformation increases the angle between x and y to 90 degrees (denoted by θ in the figure) to make it easy to identify.
I claim we can now see why the transpose must appear if we were to instead apply A to y.
Just as Ax rotates x clockwise, so, too, does, Ay rotate y clockwise (and by the same amount). The effect of applying A to y is shown at lower left. As you can see with your eyeballs, the angle between x and y has decreased rather than increased. As such, <x,Ay> =/= <Ax,y>.
However, if we apply AT to y that rotates y clockwise because the transpose of an orthogonal matrix is the inverse and the inverse of a rotation is the rotation in the other direction. That effect is shown at lower right in the figure.
Comparing results at lower right to those at upper right, we see that the angle between the the transformed vectors (θ) is the same. That is, <Ax,y> = <x,ATy>.
So there ya go. An easy-to-remember demonstration why the transpose appears when the transformation is moved to the other vector in a dot product.
There's probably something I should write here about dual spaces and Hermitians and conjugates, but imma let you look that stuff up on your own. (Look at you, looking stuff up on your own!)


No comments:
Post a Comment